Базовое рисование в PyCairo [Урок №3]

В этой части курса PyCairo, мы нарисуем несколько базовых примитивов. Мы воспользуемся операциями заливки и обводки, пунктир, окончаниями линий и их изгибы.

Линии

Линия является базовым векторным объектом. Для того, чтобы нарисовать линию, мы применим два метода. Начало линии определяется методом move_to() . Конец линии определяется методом line_to() .

#!/usr/bin/python

from gi.repository import Gtk, Gdk
import cairo


class MouseButtons:
    
    LEFT_BUTTON = 1
    RIGHT_BUTTON = 3
    
    
class Example(Gtk.Window):

    def __init__(self):
        super(Example, self).__init__()
        self.init_ui()
        
        
    def init_ui(self):    

        self.darea = Gtk.DrawingArea()
        self.darea.connect("draw", self.on_draw)
        self.darea.set_events(Gdk.EventMask.BUTTON_PRESS_MASK)        
        self.add(self.darea)
        
        self.coords = []
                     
        self.darea.connect("button-press-event", self.on_button_press)

        self.set_title("Lines")
        self.resize(300, 200)
        self.set_position(Gtk.WindowPosition.CENTER)
        self.connect("delete-event", Gtk.main_quit)
        self.show_all()
        
    
    def on_draw(self, wid, cr):

        cr.set_source_rgb(0, 0, 0)
        cr.set_line_width(0.5)
        
        for i in self.coords:
            for j in self.coords:
                
                cr.move_to(i[0], i[1])
                cr.line_to(j[0], j[1]) 
                cr.stroke()

        del self.coords[:]            
                         
                         
    def on_button_press(self, w, e):
        
        if e.type == Gdk.EventType.BUTTON_PRESS \
            and e.button == MouseButtons.LEFT_BUTTON:
            
            self.coords.append([e.x, e.y])
            
        if e.type == Gdk.EventType.BUTTON_PRESS \
            and e.button == MouseButtons.RIGHT_BUTTON:
            
            self.darea.queue_draw()           
                                                        
    
def main():
    
    app = Example()
    Gtk.main()
        
        
if __name__ == "__main__":    
    main()

#!/usr/bin/python

from gi.repository import Gtk, Gdk

import cairo

class MouseButtons:

LEFT_BUTTON = 1

RIGHT_BUTTON = 3

class Example(Gtk.Window):

def __init__(self):

super(Example, self).__init__()

self.init_ui()

def init_ui(self):

self.darea = Gtk.DrawingArea()

self.darea.connect("draw", self.on_draw)

self.darea.set_events(Gdk.EventMask.BUTTON_PRESS_MASK)

self.add(self.darea)

self.coords = []

self.darea.connect("button-press-event", self.on_button_press)

self.set_title("Lines")

self.resize(300, 200)

self.set_position(Gtk.WindowPosition.CENTER)

self.connect("delete-event", Gtk.main_quit)

self.show_all()

def on_draw(self, wid, cr):

cr.set_source_rgb(0, 0, 0)

cr.set_line_width(0.5)

for i in self.coords:

for j in self.coords:

cr.move_to(i[0], i[1])

cr.line_to(j[0], j[1])

cr.stroke()

del self.coords[:]

def on_button_press(self, w, e):

if e.type == Gdk.EventType.BUTTON_PRESS \

and e.button == MouseButtons.LEFT_BUTTON:

self.coords.append([e.x, e.y])

if e.type == Gdk.EventType.BUTTON_PRESS \

and e.button == MouseButtons.RIGHT_BUTTON:

self.darea.queue_draw()

def main():

app = Example()

Gtk.main()

if __name__ == "__main__":

main()

В нашем примере мы в случайном порядке нажимаем левой кнопкой мыши в окне. Каждое нажатие сохраняется в списке. При нажатии правой кнопкой мыши в окне, все точки соединяются со всеми точками, указанными в списке. Повторное нажатие правой кнопкой мыши очищает окно.

class MouseButtons:
    
    LEFT_BUTTON = 1
    RIGHT_BUTTON = 3

class MouseButtons:

LEFT_BUTTON = 1

RIGHT_BUTTON = 3

Документация GTK указывает на то, что левая кнопка мыши у нас находится под номером 1, правая кнопка мыши под номером 3. Мы создадим собственный класс, чтобы обозначить клавиши мыши собственными идентификаторами.

self.darea.set_events(Gdk.EventMask.BUTTON_PRESS_MASK)

1	self.darea.set_events(Gdk.EventMask.BUTTON_PRESS_MASK)

Некоторые действия не указаны по умолчанию, это касается и действий, вызванных нажатием мыши. Нам нужно указать действия, вызванные нажатием мыши при помощи метода the set_event() .

self.darea.connect("button-press-event", self.on_button_press)

1	self.darea.connect("button-press-event", self.on_button_press)

При помощи данного кода, мы получаем реакцию на действия, вызванные нажатием мыши.

cr.set_source_rgb(0, 0, 0)
cr.set_line_width(0.5)

1 2	cr.set_source_rgb(0, 0, 0) cr.set_line_width(0.5)

Линии написаны черным цветом с толщиной 0.5 точки.

for i in self.coords:
    for j in self.coords:
        
        cr.move_to(i[0], i[1])
        cr.line_to(j[0], j[1]) 
        cr.stroke()

for i in self.coords:

for j in self.coords:

cr.move_to(i[0], i[1])

cr.line_to(j[0], j[1])

cr.stroke()

Мы связываем каждую точку в списке со всеми остальными. Метод stroke() рисует указанную линию.

del self.coords[:]

1	del self.coords[:]

В конце все координаты удаляются, и мы можем приступить к новому объекту.

def on_button_press(self, w, e):
    
    if e.type == Gdk.EventType.BUTTON_PRESS \
        and e.button == MouseButtons.LEFT_BUTTON:
        
        self.coords.append([e.x, e.y])
...

def on_button_press(self, w, e):

if e.type == Gdk.EventType.BUTTON_PRESS \

and e.button == MouseButtons.LEFT_BUTTON:

self.coords.append([e.x, e.y])

...

При нажатии левой клавиши мыши, мы добавляем координаты х и у в список self.coords .

if e.type == Gdk.EventType.BUTTON_PRESS \
    and e.button == MouseButtons.RIGHT_BUTTON:
    
    self.darea.queue_draw()

if e.type == Gdk.EventType.BUTTON_PRESS \

and e.button == MouseButtons.RIGHT_BUTTON:

self.darea.queue_draw()

При нажатии правой кнопкой мыши, мы вызываем метод queue_draw() , который перерисовывает область рисования. Все точки теперь соединены с линиями.

Есть вопросы по Python?

На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!

Python Форум Помощи

Telegram Чат & Канал

Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!

Чат

Канал

Паблик VK

Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!

Заливка и Контуры

Операция мазков рисует контуры фигуры, а операция заливки заполняет пространство фигуры.

#!/usr/bin/python

from gi.repository import Gtk
import cairo
import math


class Example(Gtk.Window):

    def __init__(self):
        super(Example, self).__init__()
        
        self.init_ui()
        
        
    def init_ui(self):    

        darea = Gtk.DrawingArea()
        darea.connect("draw", self.on_draw)
        self.add(darea)

        self.set_title("Fill & stroke")
        self.resize(230, 150)
        self.set_position(Gtk.WindowPosition.CENTER)
        self.connect("delete-event", Gtk.main_quit)
        self.show_all()
        
    
    def on_draw(self, wid, cr):

        cr.set_line_width(9)
        cr.set_source_rgb(0.7, 0.2, 0.0)
        
        w, h = self.get_size()      

        cr.translate(w/2, h/2)
        cr.arc(0, 0, 50, 0, 2*math.pi)
        cr.stroke_preserve()
        
        cr.set_source_rgb(0.3, 0.4, 0.6)
        cr.fill()
        
    
def main():
    
    app = Example()
    Gtk.main()
        
        
if __name__ == "__main__":    
    main()

#!/usr/bin/python

from gi.repository import Gtk

import cairo

import math

class Example(Gtk.Window):

def __init__(self):

super(Example, self).__init__()

self.init_ui()

def init_ui(self):

darea = Gtk.DrawingArea()

darea.connect("draw", self.on_draw)

self.add(darea)

self.set_title("Fill & stroke")

self.resize(230, 150)

self.set_position(Gtk.WindowPosition.CENTER)

self.connect("delete-event", Gtk.main_quit)

self.show_all()

def on_draw(self, wid, cr):

cr.set_line_width(9)

cr.set_source_rgb(0.7, 0.2, 0.0)

w, h = self.get_size()

cr.translate(w/2, h/2)

cr.arc(0, 0, 50, 0, 2*math.pi)

cr.stroke_preserve()

cr.set_source_rgb(0.3, 0.4, 0.6)

cr.fill()

def main():

app = Example()

Gtk.main()

if __name__ == "__main__":

main()

В данном примере мы нарисуем круг и зальем его сплошным цветом.

import math

1	import math

Данный модуль нужен для константы pi , которая применяется при рисовании круга.

cr.set_line_width(9)
cr.set_source_rgb(0.7, 0.2, 0.0)

1 2	cr.set_line_width(9) cr.set_source_rgb(0.7, 0.2, 0.0)

Мы указываем ширину линии при помощи метода set_line_width() . При помощи метода set_source_rgb() мы применяем, в данном случае, темно-красный цвет.

w, h = self.get_size()

1	w, h = self.get_size()

Таким образом, мы указываем ширину и высоту окна. Нам нужны эти данные для указания центра круга в окне.

cr.translate(w/2, h/2)
cr.arc(0, 0, 50, 0, 2*math.pi)
cr.stroke_preserve()

cr.translate(w/2, h/2)

cr.arc(0, 0, 50, 0, 2*math.pi)

cr.stroke_preserve()

Нам нужно, чтобы наш круг находился строго по центру для этого используем метод translate(). Метод arc() добавляет новый путь окружности к контексту рисования Cairo. Наконец, метод stroke_preserve() описывает контур круга. В отличии от метода stroke() , он также сохраняет форму для будущего рисунка.

cr.set_source_rgb(0.3, 0.4, 0.6)
cr.fill()

1 2	cr.set_source_rgb(0.3, 0.4, 0.6) cr.fill()

Мы меняем цвет рисунка и выполняем заливку круга новым цветом при помощи метода fill() .

Пунктирные линии

Каждая линия может быть нарисована с различными пунктирными прочерками. Пунктир определяет стиль линии. Шаблон пунктира применяется при помощи модуля set_dash() . Шаблон задается списком тире, список является набором «плавающих» вариантов пунктира. С их помощью отображаются, либо же скрываются части шаблона пунктира.

Тот или иной пунктир указывается методом stroke() для создания линии. Если количество пунктирных линий указано как 0, то пунктирование отключается и линия будет сплошной. Если количество пунктирных линий указано как 1, то шаблон применяется с симметричным чередованием частей размера, в соответствии с указанным размером пунктирной линии.

def on_draw(self, wid, cr):

    cr.set_source_rgba(0, 0, 0, 1)
    cr.set_line_width(2)

    cr.set_dash([4.0, 21.0, 2.0])

    cr.move_to(40, 30)  
    cr.line_to(250, 30)
    cr.stroke()

    cr.set_dash([14.0, 6.0])

    cr.move_to(40, 50)
    cr.line_to(250, 50)
    cr.stroke()

    cr.set_dash([1.0])

    cr.move_to(40, 70)
    cr.line_to(250, 70)
    cr.stroke()

def on_draw(self, wid, cr):

cr.set_source_rgba(0, 0, 0, 1)

cr.set_line_width(2)

cr.set_dash([4.0, 21.0, 2.0])

cr.move_to(40, 30)

cr.line_to(250, 30)

cr.stroke()

cr.set_dash([14.0, 6.0])

cr.move_to(40, 50)

cr.line_to(250, 50)

cr.stroke()

cr.set_dash([1.0])

cr.move_to(40, 70)

cr.line_to(250, 70)

cr.stroke()

Мы рисуем три линии с тремя разными пунктирами.

cr.set_dash([4.0, 21.0, 2.0])

1	cr.set_dash([4.0, 21.0, 2.0])

У нас есть шаблоны из трех чисел. С начала линии 4 точки отображаются, следующие 21 не отображаются, следующие 2 отображаются, затем следующие 4 точки не отображаются, следующие 21 точка отображается и следующие 2 точки не отображаются. Данный шаблон применяется от начала и до конца линии.

cr.set_dash([14.0, 6.0])

1	cr.set_dash([14.0, 6.0])

В данном шаблоне 14 точек отображаются, затем следующие 6 точек не отображаются

cr.set_dash([1.0])

1	cr.set_dash([1.0])

Мы создали симметричный шаблон пунктирной линии с чередующимися отображаемыми и не отображаемыми точками.

Окончания линий

Окончания линий означают конечную точку нашей линии.

cairo.LINE_CAP_BUTT
cairo.LINE_CAP_ROUND
cairo.LINE_CAP_SQUARE

В Cairo существует три разных окончания линий с разными стилями.

Линия с окончанием cairo.LINE_CAP_SQUARE имеет отличный от cairo.LINE_CAP_BUTT размер. Если линия имеет ширину х единиц, линия с окончанием cairo.LINE_CAP_SQUARE будет иметь ширину х\2 в начале и конце.

def on_draw(self, wid, cr):

    cr.set_source_rgba(0, 0, 0, 1)
    cr.set_line_width(12)

    cr.set_line_cap(cairo.LINE_CAP_BUTT)
    cr.move_to(30, 50)
    cr.line_to(150, 50)
    cr.stroke()

    cr.set_line_cap(cairo.LINE_CAP_ROUND)
    cr.move_to(30, 90)
    cr.line_to(150, 90)
    cr.stroke()

    cr.set_line_cap(cairo.LINE_CAP_SQUARE)
    cr.move_to(30, 130)
    cr.line_to(150, 130)
    cr.stroke()

    cr.set_line_width(1.5)

    cr.move_to(30, 35)
    cr.line_to(30, 145)
    cr.stroke()

    cr.move_to(150, 35)
    cr.line_to(150, 145)
    cr.stroke()

    cr.move_to(155, 35)
    cr.line_to(155, 145)
    cr.stroke()

def on_draw(self, wid, cr):

cr.set_source_rgba(0, 0, 0, 1)

cr.set_line_width(12)

cr.set_line_cap(cairo.LINE_CAP_BUTT)

cr.move_to(30, 50)

cr.line_to(150, 50)

cr.stroke()

cr.set_line_cap(cairo.LINE_CAP_ROUND)

cr.move_to(30, 90)

cr.line_to(150, 90)

cr.stroke()

cr.set_line_cap(cairo.LINE_CAP_SQUARE)

cr.move_to(30, 130)

cr.line_to(150, 130)

cr.stroke()

cr.set_line_width(1.5)

cr.move_to(30, 35)

cr.line_to(30, 145)

cr.stroke()

cr.move_to(150, 35)

cr.line_to(150, 145)

cr.stroke()

cr.move_to(155, 35)

cr.line_to(155, 145)

cr.stroke()

В данном примере нарисованы три линии с тремя разными окончаниями. Это также наглядно демонстрирует разницу в размерах линий благодаря трем дополнительным тонким вертикальным линиям.

cr.set_line_width(12)

1	cr.set_line_width(12)

Толщина наших линий будет 12 единиц. Ширина линии по умолчанию – 2 единицы.

cr.set_line_cap(cairo.LINE_CAP_ROUND)
cr.move_to(30, 90)
cr.line_to(150, 90)
cr.stroke()

cr.set_line_cap(cairo.LINE_CAP_ROUND)

cr.move_to(30, 90)

cr.line_to(150, 90)

cr.stroke()

Мы нарисовали горизонтальную линию с окончанием cairo.LINE_CAP_ROUND .

cr.set_line_width(1.5)

cr.move_to(30, 35)
cr.line_to(30, 145)
cr.stroke()

cr.set_line_width(1.5)

cr.move_to(30, 35)

cr.line_to(30, 145)

cr.stroke()

Одна из трех вертикальных линий используется для демонстрации разниц в размерах.

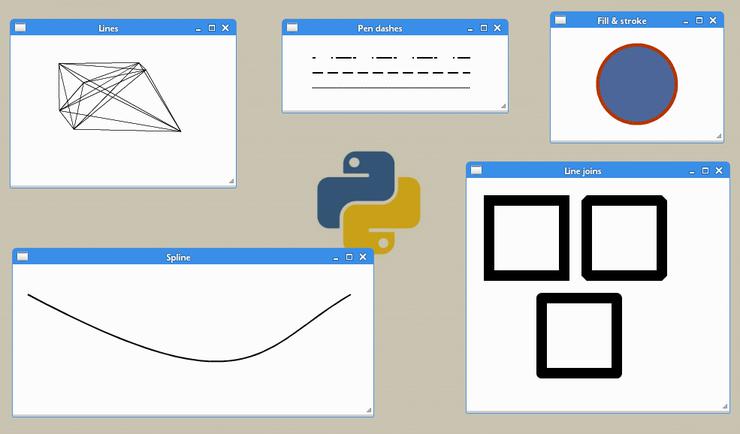
Изгибы линий

Линии могут пересекаться в трех различных стилях.

cairo.LINE_JOIN_MITER
cairo.LINE_JOIN_BEVEL
cairo.LINE_JOIN_ROUND

def on_draw(self, wid, cr):

    cr.set_line_width(14)
    
    cr.rectangle(30, 30, 100, 100)        
    cr.set_line_join(cairo.LINE_JOIN_MITER)
    cr.stroke()

    cr.rectangle(160, 30, 100, 100)
    cr.set_line_join(cairo.LINE_JOIN_BEVEL)
    cr.stroke()

    cr.rectangle(100, 160, 100, 100)
    cr.set_line_join(cairo.LINE_JOIN_ROUND)
    cr.stroke()

def on_draw(self, wid, cr):

cr.set_line_width(14)

cr.rectangle(30, 30, 100, 100)

cr.set_line_join(cairo.LINE_JOIN_MITER)

cr.stroke()

cr.rectangle(160, 30, 100, 100)

cr.set_line_join(cairo.LINE_JOIN_BEVEL)

cr.stroke()

cr.rectangle(100, 160, 100, 100)

cr.set_line_join(cairo.LINE_JOIN_ROUND)

cr.stroke()

В данном примере мы нарисуем три толстых прямоугольника с различными изгибами линий

cr.set_line_width(14)

1	cr.set_line_width(14)

Толщина линий 14 единиц.

cr.rectangle(30, 30, 100, 100)        
cr.set_line_join(cairo.LINE_JOIN_MITER)
cr.stroke()

cr.rectangle(30, 30, 100, 100)

cr.set_line_join(cairo.LINE_JOIN_MITER)

cr.stroke()

Мы нарисовали прямоугольник со стилем изгиба линий cairo.LINE_JOIN_MITER.

Кривая Безье

Кривая Безье представлена в виде кривых линий, которые указаны в соответствии с определенными математическими формулами. Математический метод расчет кривых был разработан французским математиком Пьером Безье в конце 1960-х для производства автомобилей Рено.

curve_to(x1, y1, x2, y2, x3, y3)

1	curve_to(x1, y1, x2, y2, x3, y3)

Метод curve_to() добавляет кубический сплайн в указанный путь. Параметры координат х и у первой контрольной точки, координаты х и у для второй контрольной точки и координаты х и у в конце кривой.

def on_draw(self, wid, cr):

    cr.move_to(20, 40)
    cr.curve_to(320, 200, 330, 110, 450, 40)        
    cr.stroke()

def on_draw(self, wid, cr):

cr.move_to(20, 40)

cr.curve_to(320, 200, 330, 110, 450, 40)

cr.stroke()

В данном примере кривая Безье написана с применением метода curve_to().

Vasile Buldumac

Являюсь администратором нескольких порталов по обучению языков программирования Python, Golang и Kotlin. В составе небольшой команды единомышленников, мы занимаемся популяризацией языков программирования на русскоязычную аудиторию. Большая часть статей была адаптирована нами на русский язык и распространяется бесплатно.

E-mail: vasile.buldumac@ati.utm.md

Образование
Universitatea Tehnică a Moldovei (utm.md)

2014 — 2018 Технический Университет Молдовы, ИТ-Инженер. Тема дипломной работы «Автоматизация покупки и продажи криптовалюты используя технический анализ»
2018 — 2020 Технический Университет Молдовы, Магистр, Магистерская диссертация «Идентификация человека в киберпространстве по фотографии лица»