Пример создания рекуррентной нейронной сети в Python

В данной статье мы рассмотрим, что такое рекуррентные нейронные сети и как создать нейронную сеть с нуля в Python.

Содержание

Зачем нужны рекуррентные нейронные сети
Создание рекуррентной нейронной сети на примере
Поставление задачи для рекуррентной нейронной сети
Составление плана для нейронной сети
Предварительная обработка рекуррентной нейронной сети RNN
Фаза прямого распространения нейронной сети
Фаза обратного распространения нейронной сети
Параметры рассматриваемой нейронной сети
Тестирование рекуррентной нейронной сети

Рекуррентные нейронные сети (RNN) — это тип нейронных сетей, которые специализируются на обработке последовательностей. Зачастую их используют в таких задачах, как обработка естественного языка (Natural Language Processing) из-за их эффективности в анализе текста. В данной статье мы наглядно рассмотрим рекуррентные нейронные сети, поймем принцип их работы, а также создадим одну сеть в Python, используя numpy.

Данная статья подразумевает наличие у читателя базовых знаний о нейронных сетях. Будет не лишним прочитать от том как создать нейронную сеть в Python, в которой показаны простые примеры использования нейронов в Python.

Приступим!

Зачем нужны рекуррентные нейронные сети

Один из нюансов работы с нейронными сетями (а также CNN) заключается в том, что они работают с предварительно заданными параметрами. Они принимают входные данные с фиксированными размерами и выводят результат, который также является фиксированным. Плюс рекуррентных нейронных сетей, или RNN, в том, что они обеспечивают последовательности с вариативными длинами как для входа, так и для вывода. Вот несколько примеров того, как может выглядеть рекуррентная нейронная сеть:

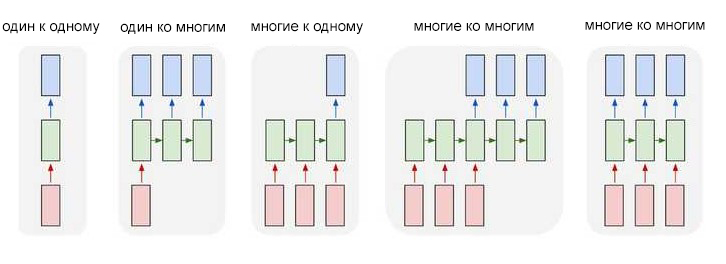
Входные данные отмечены красным, нейронная сеть RNN — зеленым, а вывод — синим.

Способность обрабатывать последовательности делает рекуррентные нейронные сети RNN весьма полезными. Области использования:

Машинный перевод (пример Google Translate) выполняется при помощи нейронных сетей с принципом «многие ко многим». Оригинальная последовательность текста подается в рекуррентную нейронную сеть, которая затем создает переведенный текст в качестве результата вывода;
Анализ настроений часто выполняется при помощи рекуррентных нейронных сетей с принципом «многие к одному». Этот отзыв положительный или отрицательный? Такая постановка является одним из примеров анализа настроений. Анализируемый текст подается нейронную сеть, которая затем создает единственную классификацию вывода. Например — Этот отзыв положительный.

Есть вопросы по Python?

На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!

Python Форум Помощи

Telegram Чат & Канал

Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!

Чат

Канал

Паблик VK

Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!

Далее в статье будет показан пример создания рекуррентной нейронной сети по схеме «многие к одному» для анализа настроений.

Создание рекуррентной нейронной сети на примере

Представим, что у нас есть нейронная сеть, которая работает по принципу «многое ко многим«. Входные данные — x₀, х₁, … x_n, а результаты вывода — y₀, y₁, … y_n. Данные x_i и y_i являются векторами и могут быть произвольных размеров.

Рекуррентные нейронные сети RNN работают путем итерированного обновления скрытого состояния h, которое является вектором, что также может иметь произвольный размер. Стоит учитывать, что на любом заданном этапе t:

Следующее скрытое состояние h_t подсчитывается при помощи предыдущего h_{t - 1} и следующим вводом x_t;
Следующий вывод y_t подсчитывается при помощи h_t.

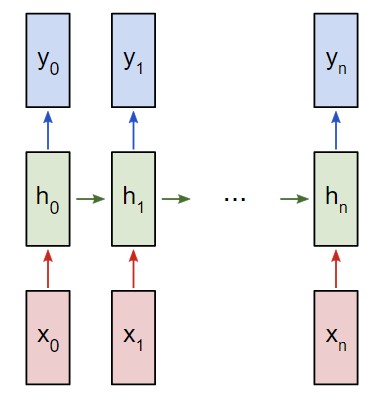Рекуррентная нейронная сеть RNN многие ко многим

Вот что делает нейронную сеть рекуррентной: на каждом шаге она использует один и тот же вес. Говоря точнее, типичная классическая рекуррентная нейронная сеть использует только три набора параметров веса для выполнения требуемых подсчетов:

W_xh используется для всех связок x_t → h_t
W_hh используется для всех связок h_t-1 → h_t
W_hy используется для всех связок h_t → y_t

Для рекуррентной нейронной сети мы также используем два смещения:

b_h добавляется при подсчете h_t
b_y добавляется при подсчете y_t

Вес будет представлен как матрица, а смещение как вектор. В данном случае рекуррентная нейронная сеть состоит их трех параметров веса и двух смещений.

Следующие уравнения являются компактным представлением всего вышесказанного:

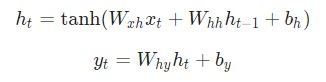
Разбор уравнений лучше не пропускать. Остановитесь на минутку и изучите их внимательно. Помните, что вес — это матрица, а другие переменные являются векторами.

Говоря о весе, мы используем матричное умножение, после чего векторы вносятся в конечный результат. Затем применяется гиперболическая функция в качестве функции активации первого уравнения. Стоит иметь в виду, что другие методы активации, например, сигмоиду, также можно использовать.

Не знаете, что такое функция активации? Вы можете ознакомиться с ними в вводной статье о нейронных сетях. Для оптимальной работы это важно.

Поставление задачи для рекуррентной нейронной сети

К текущему моменту мы смогли реализовать рекуррентную нейронную сеть RNN с нуля. Она должна выполнить простой анализ настроения. В дальнейшем примере мы попросим сеть определить, будет заданная строка нести позитивный или негативный характер.

Вот несколько примеров из небольшого набора данных, который был собран для данной статьи:

Текст	Позитивный?
Я хороший	Да
Я плохой	Нет
Это очень хорошо	Да
Это неплохо	Да
Я плохой, а не хороший	Нет
Я несчастен	Нет
Это было хорошо	Да
Я чувствую себя неплохо, мне не грустно	Да

Составление плана для нейронной сети

В следующем примере будет использована классификация рекуррентной сети «многие к одному». Принцип ее использования напоминает работу схемы «многие ко многим», что была описана ранее. Однако на этот раз будет задействовано только скрытое состояние для одного пункта вывода y:

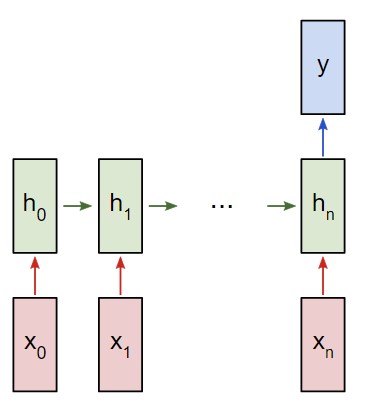
Рекуррентная нейронная сеть RNN многие к одному

Каждый x_i будет вектором, представляющим определенное слово из текста. Вывод y будет вектором, содержащим два числа. Одно представляет позитивное настроение, а второе — негативное. Мы используем функцию Softmax, чтобы превратить эти значения в вероятности, и в конечном счете выберем между позитивным и негативным.

Приступим к созданию нашей рекуррентной нейронной сети.

Предварительная обработка рекуррентной нейронной сети RNN

Упомянутый ранее набор данных состоит из двух словарей Python:

train_data = {
    'good': True,
    'bad': False,
    # ... больше данных
}

test_data = {
    'this is happy': True,
    'i am good': True,
    # ... больше данных
}

train_data = {

'good': True,

'bad': False,

# ... больше данных

}

test_data = {

'this is happy': True,

'i am good': True,

# ... больше данных

}

True = Позитивное, False = Негативное

Для получения данных в удобном формате потребуется сделать определенную предварительную обработку. Для начала необходимо создать словарь в Python из всех слов, которые употребляются в наборе данных:

from data import train_data, test_data

# Создание словаря
vocab = list(set([w for text in train_data.keys() for w in text.split(' ')]))
vocab_size = len(vocab)

print('%d unique words found' % vocab_size) # найдено 18 уникальных слов

from data import train_data, test_data

# Создание словаря

vocab = list(set([w for text in train_data.keys() for w in text.split(' ')]))

vocab_size = len(vocab)

print('%d unique words found' % vocab_size) # найдено 18 уникальных слов

vocab теперь содержит список всех слов, которые употребляются как минимум в одном учебном тексте. Далее присвоим каждому слову из vocab индекс типа integer (целое число).

# Назначить индекс каждому слову
word_to_idx = { w: i for i, w in enumerate(vocab) }
idx_to_word = { i: w for i, w in enumerate(vocab) }

print(word_to_idx['good']) # 16 (это может измениться)
print(idx_to_word[0]) # грустно (это может измениться)

# Назначить индекс каждому слову

word_to_idx = { w: i for i, w in enumerate(vocab) }

idx_to_word = { i: w for i, w in enumerate(vocab) }

print(word_to_idx['good']) # 16 (это может измениться)

print(idx_to_word[0]) # грустно (это может измениться)

Теперь можно отобразить любое заданное слово при помощи индекса целого числа. Это очень важный пункт, так как:

Рекуррентная нейронная сеть не различает слов — только числа.

Напоследок напомним, что каждый ввод x_i для рассматриваемой рекуррентной нейронной сети является вектором. Мы будем использовать веторы, которые представлены в виде унитарного кода. Единица в каждом векторе будет находиться в соответствующем целочисленном индексе слова.

Так как в словаре 18 уникальных слов, каждый x_i будет 18-мерным унитарным вектором.

import numpy as np


def createInputs(text):
    '''
    Возвращает массив унитарных векторов
    которые представляют слова в введенной строке текста
    - текст является строкой string
    - унитарный вектор имеет форму (vocab_size, 1)
    '''
    
    inputs = []
    for w in text.split(' '):
        v = np.zeros((vocab_size, 1))
        v[word_to_idx[w]] = 1
        inputs.append(v)
    
    return inputs

import numpy as np

def createInputs(text):

'''

Возвращает массив унитарных векторов

которые представляют слова в введенной строке текста

- текст является строкой string

- унитарный вектор имеет форму (vocab_size, 1)

'''

inputs = []

for w in text.split(' '):

v = np.zeros((vocab_size, 1))

v[word_to_idx[w]] = 1

inputs.append(v)

return inputs

Мы используем createInputs() позже для создания входных данных в виде векторов и последующей их передачи в рекуррентную нейронную сеть RNN.

Фаза прямого распространения нейронной сети

Пришло время для создания рекуррентной нейронной сети. Начнем инициализацию с тремя параметрами веса и двумя смещениями.

import numpy as np
from numpy.random import randn


class RNN:
    # Классическая рекуррентная нейронная сеть
    
    def __init__(self, input_size, output_size, hidden_size=64):
        # Вес
        self.Whh = randn(hidden_size, hidden_size) / 1000
        self.Wxh = randn(hidden_size, input_size) / 1000
        self.Why = randn(output_size, hidden_size) / 1000
        
        # Смещения
        self.bh = np.zeros((hidden_size, 1))
        self.by = np.zeros((output_size, 1))

import numpy as np

from numpy.random import randn

class RNN:

# Классическая рекуррентная нейронная сеть

def __init__(self, input_size, output_size, hidden_size=64):

# Вес

self.Whh = randn(hidden_size, hidden_size) / 1000

self.Wxh = randn(hidden_size, input_size) / 1000

self.Why = randn(output_size, hidden_size) / 1000

# Смещения

self.bh = np.zeros((hidden_size, 1))

self.by = np.zeros((output_size, 1))

Обратите внимание: для того, чтобы убрать внутреннюю вариативность весов, мы делим на 1000. Это не самый лучший способ инициализации весов, но он довольно простой, подойдет для новичков и неплохо работает для данного примера.

Для инициализации веса из стандартного нормального распределения мы используем np.random.randn().

Затем мы реализуем прямую передачу рассматриваемой нейронной сети. Помните первые два уравнения, рассматриваемые ранее?

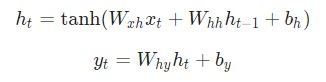
Эти же уравнения, реализованные в коде:

class RNN:
    # ...
    
    def forward(self, inputs):
        '''
        Выполнение передачи нейронной сети при помощи входных данных
        Возвращение результатов вывода и скрытого состояния
        Вывод - это массив одного унитарного вектора с формой (input_size, 1)
        '''
        h = np.zeros((self.Whh.shape[0], 1))
        
        # Выполнение каждого шага в нейронной сети RNN
        for i, x in enumerate(inputs):
            h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)
        
        # Compute the output
        y = self.Why @ h + self.by
        
        return y, h

class RNN:

# ...

def forward(self, inputs):

'''

Выполнение передачи нейронной сети при помощи входных данных

Возвращение результатов вывода и скрытого состояния

Вывод - это массив одного унитарного вектора с формой (input_size, 1)

'''

h = np.zeros((self.Whh.shape[0], 1))

# Выполнение каждого шага в нейронной сети RNN

for i, x in enumerate(inputs):

h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)

# Compute the output

y = self.Why @ h + self.by

return y, h

Довольно просто, не так ли? Обратите внимание на то, что мы инициализировали h для нулевого вектора в первом шаге, так как у нас нет предыдущего h, который теперь можно использовать.

Давайте попробуем следующее:

# ...

def softmax(xs):
    # Применение функции Softmax для входного массива
    return np.exp(xs) / sum(np.exp(xs))


# Инициализация нашей рекуррентной нейронной сети RNN
rnn = RNN(vocab_size, 2)


inputs = createInputs('i am very good')
out, h = rnn.forward(inputs)
probs = softmax(out)
print(probs) # [[0.50000095], [0.49999905]]

# ...

def softmax(xs):

# Применение функции Softmax для входного массива

return np.exp(xs) / sum(np.exp(xs))

# Инициализация нашей рекуррентной нейронной сети RNN

rnn = RNN(vocab_size, 2)

inputs = createInputs('i am very good')

out, h = rnn.forward(inputs)

probs = softmax(out)

print(probs) # [[0.50000095], [0.49999905]]

Наша рекуррентная нейронная сеть работает, однако ее с трудом можно назвать полезной. Давайте исправим этот недочет.

Фаза обратного распространения нейронной сети

Для тренировки рекуррентной нейронной сети будет использована функция потери. Здесь будет использована потеря перекрестной энтропии, которая в большинстве случаев совместима с функцией Softmax. Формула для подсчета:

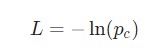
Здесь p_c является предсказуемой вероятностью рекуррентной нейронной сети для класса correct (позитивный или негативный). Например, если позитивный текст предсказывается рекуррентной нейронной сетью как позитивный текст на 90%, то потеря составит:

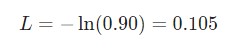
При наличии параметров потери можно натренировать нейронную сеть таким образом, чтобы она использовала градиентный спуск для минимизации потерь. Следовательно, здесь понадобятся градиенты.

Обратите внимание: следующий раздел подразумевает наличие у читателя базовых знаний об многовариантном исчислении. Вы можете пропустить несколько абзацев, однако мы рекомендуем все пробежаться по ним глазами. По мере получения новых данных код будет дополняться, и объяснения станут понятнее.

Оригиналы всех кодов, которые использованы в данной инструкции, доступны на GitHub.

Готовы? Продолжим!

Параметры рассматриваемой нейронной сети

Параметры данных, которые будут использованы в дальнейшем:

y — необработанные входные данные нейронной сети;
р — конечная вероятность: р = softmax(y);
с — истинная метка определенного образца текста, так называемый «правильный» класс;
L — потеря перекрестной энтропии: L = -ln(p_c);
W_xh, W_hh и W_hy — три матрицы веса в рассматриваемой нейронной сети;
b_h и b_y — два вектора смещения в рассматриваемой рекуррентной нейронной сети RNN.

Установка

Следующим шагом будет настройка фазы прямого распространения. Это необходимо для кеширования отдельных данных, которые будут использоваться в фазе обратного распространения нейронной сети. Параллельно с этим можно будет установить основной скелет для фазы обратного распространения. Это будет выглядеть следующим образом:

class RNN:
    # ...

    def forward(self, inputs):
        '''
        Выполнение фазы прямого распространения нейронной сети с
        использованием введенных данных.
        Возврат итоговой выдачи и скрытого состояния.
        - Входные данные в массиве однозначного вектора с формой (input_size, 1).
        '''
        h = np.zeros((self.Whh.shape[0], 1))

        self.last_inputs = inputs
        self.last_hs = { 0: h }

        # Выполнение каждого шага нейронной сети RNN
        for i, x in enumerate(inputs):
            h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)
            self.last_hs[i + 1] = h

        # Подсчет вывода
        y = self.Why @ h + self.by

        return y, h

    def backprop(self, d_y, learn_rate=2e-2):
        '''
        Выполнение фазы обратного распространения нейронной сети RNN.
        - d_y (dL/dy) имеет форму (output_size, 1).
        - learn_rate является вещественным числом float.
        '''
        pass

class RNN:

# ...

def forward(self, inputs):

'''

Выполнение фазы прямого распространения нейронной сети с

использованием введенных данных.

Возврат итоговой выдачи и скрытого состояния.

- Входные данные в массиве однозначного вектора с формой (input_size, 1).

'''

h = np.zeros((self.Whh.shape[0], 1))

self.last_inputs = inputs

self.last_hs = { 0: h }

# Выполнение каждого шага нейронной сети RNN

for i, x in enumerate(inputs):

h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)

self.last_hs[i + 1] = h

# Подсчет вывода

y = self.Why @ h + self.by

return y, h

def backprop(self, d_y, learn_rate=2e-2):

'''

Выполнение фазы обратного распространения нейронной сети RNN.

- d_y (dL/dy) имеет форму (output_size, 1).

- learn_rate является вещественным числом float.

'''

pass

Градиенты

Настало время математики! Начнем с вычисления . Что нам известно:

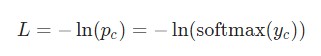
Здесь используется фактическое значение , а также применяется дифференцирование сложной функции. Результат следующий:

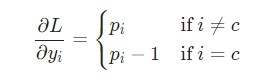
К примеру, если p = [0.2, 0.2, 0.6], а корректным классом является с = 0, то конечным результатом будет значение = [-0.8, 0.2, 0.6]. Данное выражение несложно перевести в код:

# Цикл для каждого примера тренировки
for x, y in train_data.items():
    inputs = createInputs(x)
    target = int(y)

    # Прямое распространение
    out, _ = rnn.forward(inputs)
    probs = softmax(out)

    # Создание dL/dy
    d_L_d_y = probs
    d_L_d_y[target] -= 1

    # Обратное распространение
    rnn.backprop(d_L_d_y)

# Цикл для каждого примера тренировки

for x, y in train_data.items():

inputs = createInputs(x)

target = int(y)

# Прямое распространение

out, _ = rnn.forward(inputs)

probs = softmax(out)

# Создание dL/dy

d_L_d_y = probs

d_L_d_y[target] -= 1

# Обратное распространение

rnn.backprop(d_L_d_y)

Отлично. Теперь разберемся с градиентами для W_hy и b_y, которые используются только для перехода конечного скрытого состояния в результат вывода рассматриваемой нейронной сети RNN. Используем следующие данные:

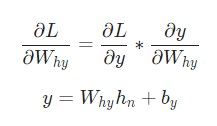
Здесь h_n является конечным скрытым состоянием. Таким образом:

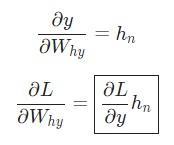
Аналогичным способом вычисляем:

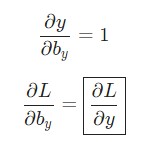
Теперь можно приступить к реализации backprop().

class RNN:
    # ...

    def backprop(self, d_y, learn_rate=2e-2):
        '''
        Выполнение фазы обратного распространения нейронной сети RNN.
        - d_y (dL/dy) имеет форму (output_size, 1).
        - learn_rate является вещественным числом float.
        '''
        n = len(self.last_inputs)

        # Подсчет dL/dWhy и dL/dby.
        d_Why = d_y @ self.last_hs[n].T
        d_by = d_y

class RNN:

# ...

def backprop(self, d_y, learn_rate=2e-2):

'''

Выполнение фазы обратного распространения нейронной сети RNN.

- d_y (dL/dy) имеет форму (output_size, 1).

- learn_rate является вещественным числом float.

'''

n = len(self.last_inputs)

# Подсчет dL/dWhy и dL/dby.

d_Why = d_y @ self.last_hs[n].T

d_by = d_y

Напоминание: мы создали self.last_hs в forward() в предыдущих примерах.

Наконец, нам понадобятся градиенты для W_hh, W_xh, и b_h, которые использовались в каждом шаге нейронной сети. У нас есть:

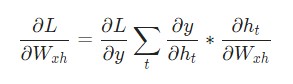
Изменение W_xh влияет не только на каждый h_t, но и на все у , что, в свою очередь, приводит к изменениям в L. Для того, чтобы полностью подсчитать градиент W_xh, необходимо провести обратное распространение через все временные шаги. Его также называют Обратным распространением во времени, или Backpropagation Through Time (BPTT):

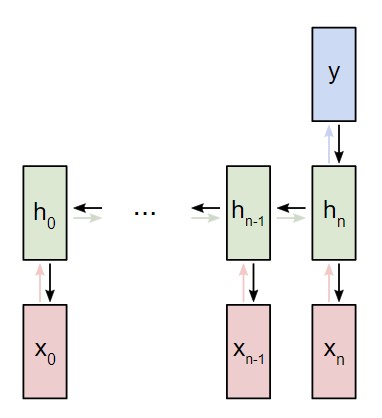Обратное распространение во времени

W_xh используется для всех прямых ссылок x_t → h_t, поэтому нам нужно провести обратное распространение назад к каждой из этих ссылок.

Приблизившись к заданному шагу t, потребуется подсчитать :

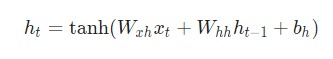
Производная гиперболической функции tanh нам уже известна:

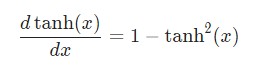
Используем дифференцирование сложной функции, или цепное правило:

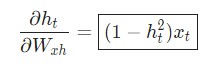
Аналогичным способом вычисляем:

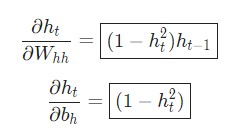
Последнее нужное значение — . Его можно подсчитать рекурсивно:

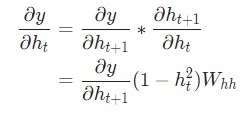
Реализуем обратное распространение во времени, или BPTT, отталкиваясь от скрытого состояния в качестве начальной точки. Далее будем работать в обратном порядке. Поэтому на момент подсчета значение будет известно. Исключением станет только последнее скрытое состояние h_n:

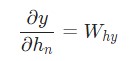
Теперь у нас есть все необходимое, чтобы наконец реализовать обратное распространение во времени ВРТТ и закончить backprop():

class RNN:
    # ...

    def backprop(self, d_y, learn_rate=2e-2):
        '''
        Выполнение фазы обратного распространения RNN.
        - d_y (dL/dy) имеет форму (output_size, 1).
        - learn_rate является вещественным числом float.
        '''
        n = len(self.last_inputs)

        # Вычисление dL/dWhy и dL/dby.
        d_Why = d_y @ self.last_hs[n].T
        d_by = d_y

        # Инициализация dL/dWhh, dL/dWxh, и dL/dbh к нулю.
        d_Whh = np.zeros(self.Whh.shape)
        d_Wxh = np.zeros(self.Wxh.shape)
        d_bh = np.zeros(self.bh.shape)

        # Вычисление dL/dh для последнего h.
        d_h = self.Why.T @ d_y

        # Обратное распространение во времени.
        for t in reversed(range(n)):
            # Среднее значение: dL/dh * (1 - h^2)
            temp = ((1 - self.last_hs[t + 1] ** 2) * d_h)

            # dL/db = dL/dh * (1 - h^2)
            d_bh += temp

            # dL/dWhh = dL/dh * (1 - h^2) * h_{t-1}
            d_Whh += temp @ self.last_hs[t].T

            # dL/dWxh = dL/dh * (1 - h^2) * x
            d_Wxh += temp @ self.last_inputs[t].T

            # Далее dL/dh = dL/dh * (1 - h^2) * Whh
            d_h = self.Whh @ temp

        # Отсекаем, чтобы предотвратить разрыв градиентов.
        for d in [d_Wxh, d_Whh, d_Why, d_bh, d_by]:
            np.clip(d, -1, 1, out=d)

        # Обновляем вес и смещение с использованием градиентного спуска.
        self.Whh -= learn_rate * d_Whh
        self.Wxh -= learn_rate * d_Wxh
        self.Why -= learn_rate * d_Why
        self.bh -= learn_rate * d_bh
        self.by -= learn_rate * d_by

class RNN:

# ...

def backprop(self, d_y, learn_rate=2e-2):

'''

Выполнение фазы обратного распространения RNN.

- d_y (dL/dy) имеет форму (output_size, 1).

- learn_rate является вещественным числом float.

'''

n = len(self.last_inputs)

# Вычисление dL/dWhy и dL/dby.

d_Why = d_y @ self.last_hs[n].T

d_by = d_y

# Инициализация dL/dWhh, dL/dWxh, и dL/dbh к нулю.

d_Whh = np.zeros(self.Whh.shape)

d_Wxh = np.zeros(self.Wxh.shape)

d_bh = np.zeros(self.bh.shape)

# Вычисление dL/dh для последнего h.

d_h = self.Why.T @ d_y

# Обратное распространение во времени.

for t in reversed(range(n)):

# Среднее значение: dL/dh * (1 - h^2)

temp = ((1 - self.last_hs[t + 1] ** 2) * d_h)

# dL/db = dL/dh * (1 - h^2)

d_bh += temp

# dL/dWhh = dL/dh * (1 - h^2) * h_{t-1}

d_Whh += temp @ self.last_hs[t].T

# dL/dWxh = dL/dh * (1 - h^2) * x

d_Wxh += temp @ self.last_inputs[t].T

# Далее dL/dh = dL/dh * (1 - h^2) * Whh

d_h = self.Whh @ temp

# Отсекаем, чтобы предотвратить разрыв градиентов.

for d in [d_Wxh, d_Whh, d_Why, d_bh, d_by]:

np.clip(d, -1, 1, out=d)

# Обновляем вес и смещение с использованием градиентного спуска.

self.Whh -= learn_rate * d_Whh

self.Wxh -= learn_rate * d_Wxh

self.Why -= learn_rate * d_Why

self.bh -= learn_rate * d_bh

self.by -= learn_rate * d_by

Моменты, на которые стоит обратить внимание:

Мы объединили 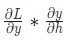в 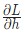для удобства;
Мы постоянно обновляем переменную d_h, которая держит самую последнюю версию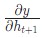 , что требуется для подсчета ;
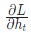Закончив с обратным распространением во времени ВРТТ, мы используем np.clip() на значениях градиента ниже -1 или выше 1. Это поможет избавиться от проблемы со взрывными градиентами. Такое случается, когда градиенты становятся слишком большими из-за огромного количества умноженных параметров. Взрыв, а также исчезновение градиентов не считается редкостью для классических рекуррентных нейронных сетей. Более сложные рекуррентные нейронные сети, например LSTM, лучше подойдут для их обработки.
Когда все градиенты подсчитаны, мы обновляем параметры веса и смещения, используя градиентный спуск.

Мы сделали это! Наша рекуррентная нейронная сеть готова.

Тестирование рекуррентной нейронной сети

Наконец настал тот момент, которого мы так долго ждали — протестируем готовую рекуррентную нейронную сеть.

Для начала, напишем вспомогательную функцию для обработки данных рассматриваемой рекуррентной нейронной сети:

import random


def processData(data, backprop=True):
    '''
    Возврат потери рекуррентной нейронной сети и точности для данных
    - данные представлены как словарь, что отображает текст как True или False.
    - backprop определяет, нужно ли использовать обратное распределение
    '''
    items = list(data.items())
    random.shuffle(items)

    loss = 0
    num_correct = 0

    for x, y in items:
        inputs = createInputs(x)
        target = int(y)

        # Прямое распределение
        out, _ = rnn.forward(inputs)
        probs = softmax(out)

        # Вычисление потери / точности 
        loss -= np.log(probs[target])
        num_correct += int(np.argmax(probs) == target)

        if backprop:
            # Создание dL/dy
            d_L_d_y = probs
            d_L_d_y[target] -= 1

            # Обратное распределение
            rnn.backprop(d_L_d_y)

    return loss / len(data), num_correct / len(data)

import random

def processData(data, backprop=True):

'''

Возврат потери рекуррентной нейронной сети и точности для данных

- данные представлены как словарь, что отображает текст как True или False.

- backprop определяет, нужно ли использовать обратное распределение

'''

items = list(data.items())

random.shuffle(items)

loss = 0

num_correct = 0

for x, y in items:

inputs = createInputs(x)

target = int(y)

# Прямое распределение

out, _ = rnn.forward(inputs)

probs = softmax(out)

# Вычисление потери / точности

loss -= np.log(probs[target])

num_correct += int(np.argmax(probs) == target)

if backprop:

# Создание dL/dy

d_L_d_y = probs

d_L_d_y[target] -= 1

# Обратное распределение

rnn.backprop(d_L_d_y)

return loss / len(data), num_correct / len(data)

Теперь можно написать цикл для тренировки сети:

# Цикл тренировки
for epoch in range(1000):
    train_loss, train_acc = processData(train_data)

    if epoch % 100 == 99:
        print('--- Epoch %d' % (epoch + 1))
        print('Train:\tLoss %.3f | Accuracy: %.3f' % (train_loss, train_acc))

        test_loss, test_acc = processData(test_data, backprop=False)
        print('Test:\tLoss %.3f | Accuracy: %.3f' % (test_loss, test_acc))

# Цикл тренировки

for epoch in range(1000):

train_loss, train_acc = processData(train_data)

if epoch % 100 == 99:

print('--- Epoch %d' % (epoch + 1))

print('Train:\tLoss %.3f | Accuracy: %.3f' % (train_loss, train_acc))

test_loss, test_acc = processData(test_data, backprop=False)

print('Test:\tLoss %.3f | Accuracy: %.3f' % (test_loss, test_acc))

Результат вывода main.py выглядит следующим образом:

--- Epoch 100
Train:  Loss 0.688 | Accuracy: 0.517
Test:   Loss 0.700 | Accuracy: 0.500
--- Epoch 200
Train:  Loss 0.680 | Accuracy: 0.552
Test:   Loss 0.717 | Accuracy: 0.450
--- Epoch 300
Train:  Loss 0.593 | Accuracy: 0.655
Test:   Loss 0.657 | Accuracy: 0.650
--- Epoch 400
Train:  Loss 0.401 | Accuracy: 0.810
Test:   Loss 0.689 | Accuracy: 0.650
--- Epoch 500
Train:  Loss 0.312 | Accuracy: 0.862
Test:   Loss 0.693 | Accuracy: 0.550
--- Epoch 600
Train:  Loss 0.148 | Accuracy: 0.914
Test:   Loss 0.404 | Accuracy: 0.800
--- Epoch 700
Train:  Loss 0.008 | Accuracy: 1.000
Test:   Loss 0.016 | Accuracy: 1.000
--- Epoch 800
Train:  Loss 0.004 | Accuracy: 1.000
Test:   Loss 0.007 | Accuracy: 1.000
--- Epoch 900
Train:  Loss 0.002 | Accuracy: 1.000
Test:   Loss 0.004 | Accuracy: 1.000
--- Epoch 1000
Train:  Loss 0.002 | Accuracy: 1.000
Test:   Loss 0.003 | Accuracy: 1.000

--- Epoch 100

Train: Loss 0.688 | Accuracy: 0.517

Test: Loss 0.700 | Accuracy: 0.500

--- Epoch 200

Train: Loss 0.680 | Accuracy: 0.552

Test: Loss 0.717 | Accuracy: 0.450

--- Epoch 300

Train: Loss 0.593 | Accuracy: 0.655

Test: Loss 0.657 | Accuracy: 0.650

--- Epoch 400

Train: Loss 0.401 | Accuracy: 0.810

Test: Loss 0.689 | Accuracy: 0.650

--- Epoch 500

Train: Loss 0.312 | Accuracy: 0.862

Test: Loss 0.693 | Accuracy: 0.550

--- Epoch 600

Train: Loss 0.148 | Accuracy: 0.914

Test: Loss 0.404 | Accuracy: 0.800

--- Epoch 700

Train: Loss 0.008 | Accuracy: 1.000

Test: Loss 0.016 | Accuracy: 1.000

--- Epoch 800

Train: Loss 0.004 | Accuracy: 1.000

Test: Loss 0.007 | Accuracy: 1.000

--- Epoch 900

Train: Loss 0.002 | Accuracy: 1.000

Test: Loss 0.004 | Accuracy: 1.000

--- Epoch 1000

Train: Loss 0.002 | Accuracy: 1.000

Test: Loss 0.003 | Accuracy: 1.000

Неплохо для рекуррентной нейронной сети, которую мы построили сами!

Хотите поэкспериментировать с этим кодом сами? Можете запустить данную рекуррентную нейронную сеть RNN у себя в браузере. Она также доступна на GitHub.

Подведем итоги

Вот и все, пошаговое руководство по рекуррентным нейронным сетям на этом закончено. Мы узнали, что такое RNN, как они работают, почему они полезны, как их создавать и тренировать. Это очень малый аспект мира нейронных сетей. При желании вы можете продолжить изучение темы самостоятельно, используя следующие ресурсы:

Подробнее ознакомьтесь с LTSM. Это долгая краткосрочная память, которая характерна более мощной архитектурой рекуррентных нейронных сетей. Будет не лишним ознакомиться с управляемым рекуррентными блоками, или GRU. Это наиболее популярная вариация LTSM;
Поэкспериментируйте с более крупными и сложными RNN. Для этого используйте подходящие ML библиотеки, например, Tensorflow, Keras или PyTorch;
Прочтите о двунаправленных нейронных сетях, которые обрабатывают последовательности как в прямом, так и в обратном направлении. Это позволяет получить больше информации на уровне вывода;
Ознакомьтесь с векторными представлением слов. Для этого можно использовать GloVe или Word2Vec;
Познакомьтесь поближе с Natural Language Toolkit (NLTK), популярной библиотекой Python для работы с данными на языках, которые используют люди, а не машины.

Благодарим за внимание!

Vasile Buldumac

Являюсь администратором нескольких порталов по обучению языков программирования Python, Golang и Kotlin. В составе небольшой команды единомышленников, мы занимаемся популяризацией языков программирования на русскоязычную аудиторию. Большая часть статей была адаптирована нами на русский язык и распространяется бесплатно.

E-mail: vasile.buldumac@ati.utm.md

Образование
Universitatea Tehnică a Moldovei (utm.md)

2014 — 2018 Технический Университет Молдовы, ИТ-Инженер. Тема дипломной работы «Автоматизация покупки и продажи криптовалюты используя технический анализ»
2018 — 2020 Технический Университет Молдовы, Магистр, Магистерская диссертация «Идентификация человека в киберпространстве по фотографии лица»