Насколько случайны случайности? Это странный вопрос, но желательно его задать, если речь идет об информационной безопасности. Когда вы генерируете случайные данные, числа или строки в Python, неплохо иметь хотя бы приблизительное представление о том, как именно генерируются эти данные.
Содержание:
- Почему случайность — случайная?
- Что значит “Криптографически безопасно”?
- Что вы из этого почерпнете?
- PRNG в Python
- Модуль random
- PRNG для массивов: numpy.random
- CSRPNG в Python
- os.urandom(): настолько случайно, насколько возможно
- Python умеет хранить секреты
- Последний кандидат: uuid
- Почему бы просто не использовать SystemRandom по умолчанию?
- Коэффициенты и окончания: Хеширование
- Подведем итоги
Здесь мы рассмотрим несколько различных способов генерации данных в Python и перейдем к их сравнению в таких категориях, как безопасность, универсальность, предназначение и скорость.
Мы обещаем, что данное руководство не будет похоже на урок математики, или криптографии: математики здесь будет ровно столько, сколько необходимо!
Насколько случайны случайности?
Во первых, нужно сделать небольшое заявление. Большая часть случайных данных, сгенерированных в Python — не совсем “случайная” в научном понимании слова. Скорее, это псевдослучайность, сгенерированная генератором псевдослучайных чисел (PRNG), который по сути, является любым алгоритмом для генерации на первый взгляд случайных, но все еще воспроизводимых данных.
“Настоящие” случайные числа могут быть сгенерированы при помощи (как вы, скорее всего, можете догадаться), настоящим генератором случайных чисел (true random number generator, TRNG). Пример: регулярно поднимать игральный кубик с пола, подбрасывать его в воздух и дать ему приземлиться.
Представим, что вы совершаете бросок произвольно и понятия не имеете, какое число выпадет на кубике. Бросок кубика — это грубая форма использования аппаратного обеспечения для генерации числа, которое не является детерминированным. TRNG выходит за рамки этой статьи, однако это стоит упомянуть в любом случае, хотя бы для сравнения.
PRNG, выполняемые обычно программным, а не аппаратным обеспечением, немного отличаются. Вот краткое описание:
Они начинают со случайного числа, также известного как зерно и затем используют алгоритм для генерации псевдослучайной последовательности битов, основанных на нём.
В какой-то момент вам могут посоветовать почитать документацию. И эти люди не то, что ошибутся. Вот интересный сниппет из документации модуля random, который вам не стоит упускать:
Внимание: псевдослучайные генераторы этого модуля не должны быть использованы в целях безопасности (источник).
Возможно, вы уже сталкивались с random.seed(999), random.seed(1234), или им подобным. Этот вызов функции проходит через генератор случайных чисел, который используется модулем random Python. Это то, что делает последующие вызовы генератора случайных чисел детерминированными: вход А производит выход Б. Это чудо может стать проклятием, если используется неправильно.
Возможно термины “случайный” и “детерминированный” выглядят так, будто не могут упоминаться в одном контексте. Чтобы прояснить этот момент, вот супер упрощенная версия random(), которая итеративно создает “случайное” число, используя x = (x * 3) % 19.
“Х” изначально определен как значение сид (cлучайное начальное значение), после чего превращается в детерминированную последовательность чисел, основанных на этом семени:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
class NotSoRandom(object): def seed(self, a=3): """Самый загадочный генератор случайных чисел в мире.""" self.seedval = a def random(self): """Смотрите, случайные числа!""" self.seedval = (self.seedval * 3) % 19 return self.seedval _inst = NotSoRandom() seed = _inst.seed random = _inst.random |
Не стоит воспринимать этот пример слишком буквально, так как он служит чисто для отображения концепции. Если вы используете значение сид 1234, дальнейшая последовательность вызовов random() всегда должна быть идентичной:
|
1 2 3 4 5 6 7 |
>>> seed(1234) >>> [random() for _ in range(10)] [16, 10, 11, 14, 4, 12, 17, 13, 1, 3] >>> seed(1234) >>> [random() for _ in range(10)] [16, 10, 11, 14, 4, 12, 17, 13, 1, 3] |
Мы рассмотрим более серьезную иллюстрацию данного примера в дальнейшем.
Что значит “криптографически безопасно”?
Если вам казалось, что в статье мало акронимов типа “RNG” — то добавим сюда еще один: CSPRNG — криптографически безопасный PRNG. CSPRNG подходят для генерации конфиденциальных данных, таких как пароли, аутентификаторы и токены. Благодаря заданной случайно строке, условный злодей не сможет определить, какая строка шла за или перед этой строкой в последовательности случайных строк.
Еще один термин, с которым вы можете столкнуться — энтропия. В двух словах, она ссылается на количество случайностей, желаемых или введенных. Например, один модуль Python, который мы рассмотрим в данной статье, определяет DEFAULT_ENTROPY = 32, количество возвращаемых байтов по умолчанию. Разработчики считают это количество байтов “достаточным”.
Обратите внимание: В данной статье я предполагаю, что байт ссылается на 8 битов, как в далеких 60-х, а не к какой-либо другой единице хранения. Можете называть его октетом, если хотите.
Главная суть CSPRNG — это то, что они все еще псевдослучайные. Они сконструированы таким образом, что являются внутренне детерминированными, но добавляют некие другие переменные, или имеют определенную собственность, которая делает их “достаточно случайными”, чтобы запретить поддержку любой функции, которая выполняет детерменизм.
Что вы из этого почерпнете?
Практически, это значит, что вам нужно использовать PRNG для статистического моделирования, симуляции и сделать случайные данные воспроизводимыми. PRNG также значительно быстрее, чем CSPRNG, что вы и увидите в дальнейшем. Используйте CSPRNG для безопасности и в криптографических приложениях, где конфиденциальные данные являются обязательным условием.
В дополнение к расширению использования вышеупомянутых примеров в этой статье, вы познакомитесь с инструментами Python для работы как с PRNG, так и с CSPRNG:
- Опции PRNG включают в себя модуль random из стандартной библиотеки Python, а также основанную на массивах копию NumPy, под названием numpy.random
- Модули Python, такие как os, secrets, и uuid содержат функции для генерации криптографически безопасных объектов.
Мы рассмотрим все вышеперечисленное и подытожим детальным сравнением.
PRNG в Python
Модуль random
Возможно самый известный инструмент для генерации случайных данных в Python — это модуль random, который использует алгоритм PRNG под названием Mersenne Twister в качестве корневого генератора.
Ранее, мы затронули random.seed(), и теперь настало подходящее время, чтобы узнать, как он работает. Сначала, давайте создадим случайные данные без сидинга. Функция random.random() возвращает случайное десятичное число с интервалом [0.0, 1.0). В результате всегда будет меньше, чем правая конечная точка (1.0). Это также известно, как полуоткрытый диапазон:
|
1 2 3 4 5 6 7 |
>>> # Пока не вызываем random.seed() >>> import random >>> random.random() 0.35553263284394376 >>> random.random() 0.6101992345575074 |
Если вы запустите этот код лично, весьма вероятно, что полученные числа на вашем компьютере будут другими. По умолчанию, когда вы не используете сид генератор, вы используете текущее системное время, или “источник случайности” вашей операционной системы, если это доступно.
С random.seed() вы можете сделать результаты воспроизводимыми, и цепочка вызова, после random.seed(), будет генерировать один и тот же след данных:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
>>> random.seed(444) >>> random.random() 0.3088946587429545 >>> random.random() 0.01323751590501987 >>> random.seed(444) # Re-seed >>> random.random() 0.3088946587429545 >>> random.random() 0.01323751590501987 |
Обратите внимание на повторение “случайных” чисел. Последовательность случайных чисел становится детерменированной, или полностью определенной значением сида, 444.
Давайте рассмотрим основы того, как функционирует модуль random. Ранее мы создали случайное десятичное число. Вы можете сгенерировать случайное целое число между двумя отметками в Python при помощи функции random.randint(). Таким образом охватывается целый интервал [x, y] и обе конечные точки могут быть включены:
|
1 2 3 4 5 |
>>> random.randint(0, 10) 7 >>> random.randint(500, 50000) 18601 |
С random.randrange(), вы можете исключить правую часть интервала, то есть сгенерированное число всегда остается внутри [x, y) и всегда будет меньше правой части:
|
1 2 |
>>> random.randrange(1, 10) 5 |
Если вы хотите сгенерировать случайные десятичные числа, которые находятся в определенном интервале [x, y], вы можете использовать random.uniform(), который вырывается из непрерывного равномерного распределения:
|
1 2 3 4 5 |
>>> random.uniform(20, 30) 27.42639687016509 >>> random.uniform(30, 40) 36.33865802745107 |
Чтобы взять случайный элемент из последовательности, не являющейся пустой (такой как список или кортеж), вы можете использовать random.choice(). Также есть random.choices() для выборки нескольких элементов из последовательности с заменой (дубликаты возможны):
|
1 2 3 4 5 6 7 8 |
>>> items = ['one', 'two', 'three', 'four', 'five'] >>> random.choice(items) 'four' >>> random.choices(items, k=2) ['three', 'three'] >>> random.choices(items, k=3) ['three', 'five', 'four'] |
Вы можете сделать последовательность случайной прямо на месте, при помощи random.shuffle(). Таким образом удастся обновить объект последовательности и сделать порядок элементов случайным:
|
1 2 |
>>> random.sample(items, 4) ['one', 'five', 'four', 'three'] |
Если вы не хотите делать это с изначальным списком, сначала вам может понадобиться сделать копию, а потом уже перемешать её. Вы можете создавать копии списков Python при помощи модуля copy, или просто x[:], или x.copy(), где x является списком.
Перед тем, как перейти к генерированию случайных данных в NumPy, давайте рассмотрим еще одно приложение, которое частично включено в процесс: генерация последовательности уникальных случайных строк с одинаковой длиной.
В первую очередь, это может разобраться с устройством функции. Вам нужно выбрать из “пула” символов, таких как буквы, числа, и\или знаки препинания, совмести их в одну строку, и затем проверить, является ли эта строка сгенерированной. Python работает отлично для такого типа тестирования:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import string def unique_strings(k: int, ntokens: int, pool: str=string.ascii_letters) -> set: """Generate a set of unique string tokens. k: Length of each token ntokens: Number of tokens pool: Iterable of characters to choose from For a highly optimized version: https://stackoverflow.com/a/48421303/7954504 """ seen = set() while len(seen) < ntokens: token = ''.join(random.choices(pool, k=k)) seen.add(token) return seen |
«».join() присоединяет буквы из random.choices() в простую строку, где «k» это длинна строки. Это токен добавлен в набор, который не может иметь дубликатов, и цикл while будет проходить, пока набор не будет содержать количество элементов, которое вы определили.
На заметку: Модуль string содержит ряд полезных констант: cii_lowercase, ascii_uppercase, string.punctuation, ascii_whitespace и еще много других.
Давайте проверим эту функцию:
|
1 2 3 4 5 |
>>> unique_strings(k=4, ntokens=5) {'AsMk', 'Cvmi', 'GIxv', 'HGsZ', 'eurU'} >>> unique_strings(5, 4, string.printable) {"'O*1!", '9Ien%', 'W=m7<', 'mUD|z'} |
Для хорошо настроенной версии этой функции, этот ответ Stack Overflow использует функции генератора, привязку имени и еще несколько продвинутых хитростей, чтобы создать более быструю, криптографически безопасную версию упомянутой ранее unique_strings().
PRNG для массивов: numpy.random
Одна вещь, которую вы могли заметить, заключается в том, что большинство функций из случайного числа возвращают скалярное значение (один int, float, или другой объект). Если вы хотели сгенерировать последовательность случайных чисел, один из способов достичь этого — охватить список Python:
|
1 2 3 4 5 6 |
>>> [random.random() for _ in range(5)] [0.021655420657909374, 0.4031628347066195, 0.6609991871223335, 0.5854998250783767, 0.42886606317322706] |
Есть еще один вариант, который был разработан как раз для этого. Вы можете рассматривать пакет numpy.random от NumPy как стандартный модуль random библиотеки Python, но только для массивов NumPy. (Он также имеет возможность рисовать из гораздо большего количество статистических распределений).
Обратите внимание на то, что numpy.random использует собственные PRNG, которые отделены от обычных случайных чисел. Вы не будете создавать детерминестически случайные массивы NumPy с вызовом random.seed():
|
1 2 3 |
>>> import numpy as np >>> np.random.seed(444) >>> np.set_printoptions(precision=2) # Выводим десятичное число |
Без дальнейших церемоний, вот несколько примеров, удовлетворяющих ваш аппетит:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
>>> # Возвращение примеров из стандартного нормального распределения >>> np.random.randn(5) array([ 0.36, 0.38, 1.38, 1.18, -0.94]) >>> np.random.randn(3, 4) array([[-1.14, -0.54, -0.55, 0.21], [ 0.21, 1.27, -0.81, -3.3 ], [-0.81, -0.36, -0.88, 0.15]]) >>> # `p` это возможность выбора каждого элемента >>> np.random.choice([0, 1], p=[0.6, 0.4], size=(5, 4)) array([[0, 0, 1, 0], [0, 1, 1, 1], [1, 1, 1, 0], [0, 0, 0, 1], [0, 1, 0, 1]]) |
В синтаксе для randn(d0, d1, …, dn), параметры d0, d1, …, dn являются опциональными и указывают форму итогового объекта. Здесь, np.random.randn(3, 4) создает 2d массив с 3 строками и 4 столбцами. В качестве данных будут i.i.d., что означает, что каждая точка данных создается независимо от других.
Еще одна простая операция — это создание последовательности случайных логических значений: True или False. Один из способов сделать это — использовать np.random.choice([True, False]). Однако, будет практически в 4 раза быстрее выбрать (0, 1), а затем отобразить эти целые числа в соответствующие булевские значения:
КОД # randint является [inclusive, exclusive), в отличие отrandom.randint()
КОД
|
1 2 3 4 5 |
>>> # NumPy's `randint` is [inclusive, exclusive), unlike `random.randint()` >>> np.random.randint(0, 2, size=25, dtype=np.uint8).view(bool) array([ True, False, True, True, False, True, False, False, False, False, False, True, True, False, False, False, True, False, True, False, True, True, True, False, True]) |
Что на счет генерации коррелированных данных? Скажем, вы хотите симулировать два корелированных временных ряда. Один из способов сделать — это использовать функцию multivariate_normal() нашего NumPy, которая учитывает матрицу ковариации. Другими словами, чтобы списать из одной нормальной распределенной случайной переменной, вам нужно определить ее среднее значение и дисперсию (или стандартное отклонение).
Для выборки из многомерного нормального распределения, вы определяете матрицу ковариации и средние значения, в итоге вы получите несколько взаимосвязанных рядов данных, которые разделены приблизительно нормально.
Однако, в отличие от ковариации, корреляция — это более знакомая для большинства мера, к тому же более интуитивная. Это ковариация, нормализованная продуктом стандартных отклонений, так что вы можете определить ковариацию с точки зрения корреляции и стандартного отклонения:
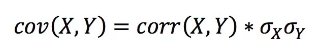
Итак, можете ли вы списать случайные выборки из многомерного нормального распределения, определив матрицу корреляции и стандартные отклонения? Да, но вам нужно будет получить приведенную выше формулу матрицы. Здесь, S — это вектор стандартных отклонений, P — это их корреляционная матрица, и С — это результирующая (квадратная) ковариационная матрица:
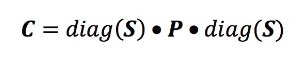
Это может быть выражено в NumPy следующим образом:
|
1 2 3 4 |
def corr2cov(p: np.ndarray, s: np.ndarray) -> np.ndarray: """Ковариационная матрица от корреляции и стандартных отклонений""" d = np.diag(s) return d @ p @ d |
Теперь, вы можете сгенерировать два временных ряда, которые коррелируют, но все еще являются случайными:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
>>> # Начало с корреляционной матрицы и стандартных отклонений >>> # -0.40 это корреляция между А и B, а корреляция >>> # самой переменной равна 1.0 >>> corr = np.array([[1., -0.40], ... [-0.40, 1.]]) >>> # Стандартные отклонения\средние арифметические А и B, соответственно >>> stdev = np.array([6., 1.]) >>> mean = np.array([2., 0.5]) >>> cov = corr2cov(corr, stdev) >>> # `size` это длина временных рядов для 2д данных >>> # (500 месяцев, дней, и так далее). >>> data = np.random.multivariate_normal(mean=mean, cov=cov, size=500) >>> data[:10] array([[ 0.58, 1.87], [-7.31, 0.74], [-6.24, 0.33], [-0.77, 1.19], [ 1.71, 0.7 ], [-3.33, 1.57], [-1.13, 1.23], [-6.58, 1.81], [-0.82, -0.34], [-2.32, 1.1 ]]) >>> data.shape (500, 2) |
Вы можете рассматривать данные как 500 пар обратно-коррелированных точек данных. Вот проверка правильности, так что вы можете вернуться к изначальному вводу, который приблизительно соответствует corr, stdev, и mean из примера выше:
|
1 2 3 4 5 6 7 8 9 |
>>> np.corrcoef(data, rowvar=False) array([[ 1. , -0.39], [-0.39, 1. ]]) >>> data.std(axis=0) array([5.96, 1.01]) >>> data.mean(axis=0) array([2.13, 0.49]) |
Перед тем как мы перейдем к CSPRNG, может быть полезно обобщить некоторые случайные функции и копии numpy.random:
| Модуль random | Аналог NumPy | Использование |
| random() | rand() | Случайное десятичное [0.0, 1.0) |
| randint(a, b) | random_integers() | Случайное целое число [a, b] |
| randrange(a, b[, step]) | randint() | Случайное целое число [a, b) |
| uniform(a, b) | uniform() | Случайное десятичное [a, b] |
| choice(seq) | choice() | Случайный элемент из seq |
| choices(seq, k=1) | choice() | Случайные k элементы из seq с заменой |
| sample(population, k) | choice() с параметром replace=False | Случайные k элементы из seq без замены |
| shuffle(x[, random]) | shuffle() | Перемешка порядка |
| normalvariate(mu, sigma) или gauss(mu, sigma) | normal() | Пример из нормального распределения со средним значением mu и стандартным отклонением sigma |
Обратите внимание: NumPy специализируется на построении и обработке больших, многомерных массивов. Если вам нужно только одно значение, то random будет достаточно, к тому же, еще и быстрее. Для небольших последовательностей, random может быть еще быстрее, так как NumPy имеет ряд дополнительных расходов.
Мы рассмотрели две фундаментальные опции PRNG, так что теперь мы можем перейти к еще более безопасным адаптациям.
CSPRNG в Python
os.urandom(): настолько случайно, на сколько возможно
Функция Python под названием os.urandom() используется как в secrets, так и в uuid (мы к ним скоро придем). Чтобы не вдаваться в лишние подробности, os.urandom() генерирует зависимые от операционной системы случайные байты, которые спокойно можно назвать криптографически надежными:
- На операционных системах Unix, она считывает случайные байты из специального файла /dev/urandom, который за раз “открывает доступ к окружающим шумам, собранным из драйверов устройств и прочих ресурсов” (спасибо, Википедия). Это искаженная информация: частично о состоянии вашего оборудования и системы в определенный момент времени, и в тоже время, значительно случайные данные;
- Для Windows, используется функция C++ под названием CryptGenRandom(). Эта функция все еще технически псевдослучайная, но работает путем генерации значения сида из переменных, таких как ID процесса, состояние памяти, и так далее;
С os.urandom() нет такого понятия, как ручной сидинг. Хотя эта функция технически является псевдослучайной, она лучше подходит под наше понимание случайности. Единственный аргумент — это количество байтов в выдаче:
|
1 2 3 4 5 6 7 8 9 |
>>> os.urandom(3) b'\xa2\xe8\x02' >>> x = os.urandom(6) >>> x b'\xce\x11\xe7"!\x84' >>> type(x), len(x) (bytes, 6) |
Перед тем как мы пойдем дальше, сейчас подходящее время для мини-урока о кодировке символов. Многие люди, как и я, имеют своего рода аллергическую реакцию, когда они видят объекты байтов и длинный ряд символов \x. Однако, будет полезным знать, как последовательности, такие как упомянутый x в итоге становятся строками и числами.
os.urandom() возвращает последовательность одиночных байтов:
|
1 2 |
>>> x b'\xce\x11\xe7"!\x84' |
Но как это в итоге превращается в строку или последовательность чисел?
Сначала нужно обратиться к фундаментальным основам вычисления, которые заключаются в том, что байт состоит из 8 битов. Вы можете воспринимать бит как одинарную цифру, которая равна либо 1, либо 0.
Байт эффективно выбирает между 0 и 1 восемь раз, так что и 01101100, и 1111000 могут представлять байты. Попробуйте следующее, чтобы увидеть, как F-строки Python представлены в вашем интерпретаторе Python 3.6:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
>>> binary = [f'{i:0>8b}' for i in range(256)] >>> binary[:16] ['00000000', '00000001', '00000010', '00000011', '00000100', '00000101', '00000110', '00000111', '00001000', '00001001', '00001010', '00001011', '00001100', '00001101', '00001110', '00001111'] |
Это эквивалент [bin(i) for i in range(256)] с определенным форматированием. bin() конвертирует целое число в его бинарное представление в качестве строки.
Что это нам дает? Использование диапазона (256) выше — это не случайный выбор. Учитывая, что мы можем использовать только 8 битов, каждый из которых имеет 2 варианта, значит мы имеем 2*8=256 возможных “комбинаций”.
Это значит, что каждый байт отображает целое число от 0 до 255. Другими словами, нам понадобится больше, чем 8 битов, чтобы выразить целое число 256. Вы можете подтвердить это, проверив, что len(f'{256:0>8b}’) теперь 9, а не 8.
Хорошо, теперь вернемся к типу данных байтов, которые мы видели выше, построив последовательность битов, соответствующую числам от 0 до 255:
|
1 |
bites = bytes(range(256)) |
Если вы вызовите list(bites), вы вернетесь к списку Python, который работает от 0 до 255. Но если вы введете байты, вы получите страшно выглядящую последовательность, заваленную лишним мусором:
|
1 2 3 4 5 6 7 |
>>> bites b'\x00\x01\x02\x03\x04\x05\x06\x07\x08\t\n\x0b\x0c\r\x0e\x0f\x10\x11\x12\x13\x14\x15' '\x16\x17\x18\x19\x1a\x1b\x1c\x1d\x1e\x1f !"#$%&\'()*+,-./0123456789:;<=>?@ABCDEFGHIJK' 'LMNOPQRSTUVWXYZ[\\]^_`abcdefghijklmnopqrstuvwxyz{|}~\x7f\x80\x81\x82\x83\x84\x85\x86' '\x87\x88\x89\x8a\x8b\x8c\x8d\x8e\x8f\x90\x91\x92\x93\x94\x95\x96\x97\x98\x99\x9a\x9b' # ... |
Эти бекслешы являются выходными последовательностями, а \xhh отображает символ с шестнадцатеричным значением hh. Некоторые элементы битов отображены буквально (печатные символы, такие как буквы, числа и знаки препинания). Большая части выражена проблеами. \x08 представляет клавишу backspace на клавиатуре, в то время как \x13 — возврат каретки (часть новой строки в системах Windows).
Если вы хотите переосмыслить шестнадцатеричный код, вот полезный комментарий Чарльза Петцольда: “Скрытый язык” — отличное место для этого. Hex — это основанная на нумерации из 16 чисел система, которая, вместо того, чтобы использовать от 0 до 9, использует от 0 до 9 и от «а» до «f» в качестве основных цифр.
Наконец, давайте вернемся к тому, где мы начинали, с последовательностью случайных байтов x. Надеюсь, так теперь будет понятнее. Вызов .hex() в байтовом объекте дает строку шестнадцатеричных чисел, каждое из которых соответствует десятичному числу от 0 до 255:
|
1 2 3 4 5 6 7 8 9 10 11 |
>>> x b'\xce\x11\xe7"!\x84' >>> list(x) [206, 17, 231, 34, 33, 132] >>> x.hex() 'ce11e7222184' >>> len(x.hex()) 12 |
Последний вопрос: каким образом b.hex() длиной 12 символов, если «х» длиной всего 6 байтов? Это связано с тем, что два шестнадцатеричных числа соответствуют одному байту. Str версия байтов всегда будет в два раза длиннее ожидаемого.
Даже если байт (такой, как \x01) не нуждается в полном наборе из 8 битов для отображения, b.hex() всегда будет использовать два числа на байт, так что номер 1 будет отображен как 01, а не просто 1. При этом математически, оба варианта получаются одинакового размера.
Техническая информация: то, что мы в основном рассмотрели здесь — это то, как объекты байтов становятся строками. Еще одна особенность заключается в том, как байты, создаваемые os.urandom(), конвертируются в десятичное число с интервалом [0.0, 1.0), как и в криптографически безопасной версии random.random(). Если вам интересно углубиться в данный вопрос, этот сниппет кода показывает, как int.from_bytes() делает начальное преобразование в целое число, используя систему с нумерацией 256.
Имея это ввиду, давайте рассмотрим предоставленный недавно модуль secrets, который делает генерацию токенов безопасности намного более удобным для пользователя.
Python умеет хранить секреты
Предоставленный одним из самых ярких PEP в Python 3.6, модуль secrets де-факто выполняет роль модуля для генерации криптографически безопасных случайных байтов и строк.
Вы можете проверить исходный код модуля, который является аккуратным и лаконичным примером 25 строк. Модуль secrets — это, по сути, обертка вокруг os.urandom(). Он экспортирует множество функций для генерации случайных чисел, байтов и строк. Большая часть этих примеров прекрасно рассказывают о себе сами:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
>>> n = 16 >>> # Создание безопасных токенов >>> secrets.token_bytes(n) b'A\x8cz\xe1o\xf9!;\x8b\xf2\x80pJ\x8b\xd4\xd3' >>> secrets.token_hex(n) '9cb190491e01230ec4239cae643f286f' >>> secrets.token_urlsafe(n) 'MJoi7CknFu3YN41m88SEgQ' >>> # Безопасная версия для `random.choice()` >>> secrets.choice('rain') 'a' |
Что на счет конкретного примера? Вы (скорее всего) пользовались сервисами сокращения URL, такими как tinyurl или bit.ly, которые превращают длинный URL в что-нибудь вроде этого: https://bit.ly/2LwO8SH. Большинство сервисов сокращения не делают никакого сложного хеширования от ввода до вывода. Они просто генерируют случайную строку, и проверяют, чтобы она не была сгенерирована ранее, и связывают её с входящим URL-ом.
Предположим, что взглянув на Root Zone Database, вы зарегистрировали сайт short.ly. Вот функция, которая поможет начать работу с вашим сервисом:
|
1 2 3 4 5 6 7 8 9 10 11 |
from secrets import token_urlsafe DATABASE = {} def shorten(url: str, nbytes: int=5) -> str: ext = token_urlsafe(nbytes=nbytes) if ext in DATABASE: return shorten(url, nbytes=nbytes) else: DATABASE.update({ext: url}) return f'short.ly/{ext} |
Является ли это развернутым изображением? Нет. Ставлю на то, что bit.ly выполняет более сложную работу, чем просто хранить свою золотую шахту в глобальном словаре Python, который не является постоянным между сеансами. Однако, это достаточно точно:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
>>> urls = ( ... 'https://realpython.com/', ... 'https://docs.python.org/3/howto/regex.html' ... ) >>> for u in urls: ... print(shorten(u)) short.ly/p_Z4fLI short.ly/fuxSyNY >>> DATABASE {'p_Z4fLI': 'https://realpython.com/', 'fuxSyNY': 'https://docs.python.org/3/howto/regex.html'} |
Погодите: Вы могли заметить одну вещь. Длина обеих результатов — 7, при том что мы запрашивали 5 байтов. Стоп, разве результат не должен быть в два раза длиннее, как и говорилось раньше? Не совсем, по крайней мере, для данного случая. Здесь происходит вот что: token_urlsafe() использует кодировку base64 , где каждый символ — это шесть битов данных. (Это от 0 до 63, плюс соответствующие символы: A-Z, a-z, 0-9, и +/.)
Если вы изначально определяете точное число байтов как nbytes, итоговая длина из secrets.token_urlsafe(nbytes) будет th.ceil(nbytes * 8 / 6), что можно доказать и исследовать, если вам любопытно.
В итоге мы имеем то, что хотя secrets — это, по сути своей, просто обертка вокруг существующих функций Python, это может пригодиться в случае, если безопасность для вас является ключевым параметром.
Последний кандидат: uuid
Последний вариант для генерации случайных токенов — это функция uuid4() из модуля uuid Python. UUID значит Universally Unique IDentifier (универсальный уникальный идентификатор), 128-битная последовательность (строка длина которой 32), разработанная для “гарантирования уникальности в пространстве и времени”. uuid4() — это одна из самых полезных функций модуля, и эта функция также использует os.urandom():
|
1 2 3 4 5 6 |
>>> import uuid >>> uuid.uuid4() UUID('3e3ef28d-3ff0-4933-9bba-e5ee91ce0e7b') >>> uuid.uuid4() UUID('2e115fcb-5761-4fa1-8287-19f4ee2877ac') |
Приятно то, что все функции uuid предоставляют экземпляр класса UUID, который инкапсулирует ID и имеет такие свойства, как .int, .bytes, и .hex:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
>>> tok = uuid.uuid4() >>> tok.bytes b'.\xb7\x80\xfd\xbfIG\xb3\xae\x1d\xe3\x97\xee\xc5\xd5\x81' >>> len(tok.bytes) 16 >>> len(tok.bytes) * 8 # In bits 128 >>> tok.hex '2eb780fdbf4947b3ae1de397eec5d581' >>> tok.int 62097294383572614195530565389543396737 |
Вы можете также столкнуться с другими вариациями: uuid1(), uuid3(), и uuid5(). Ключевая разница между ними и uuid4() в том, что эти три функции принимают ту или иную форму ввода и поэтому не соответствуют определению “случайные” в той мере, в которой делает четвертая версия UUID:
- uuid1() использует ID хост вашего компьютера в настоящее время по умолчанию. Ссылающаяся на настоящее время в наносекундном разрешении, это та версия, которая соответствует утверждению UUID “гарантированная уникальность во времени”.
- uuid3() и uuid5() принимают идентификатор пространства имен и название. Первый использует хеш MD5, второй использует SHA-1.
uuid4(), наоборот, является абсолютно псевдослучайным (или случайным). Функция являет собой использование 16 байтов для os.urandom(), конвертируя их в целое число и выполняет ряд поразрядных операций согласно формальной спецификации.
Надеюсь, теперь у вас есть более точное понимание различия между “типами” случайных данных и как они создаются. Однако, есть другая проблема, которая может возникнуть — это столкновения.
В нашем случае, столкновение может просто ссылаться к генерации двух соответствующих UUID. Каковы шансы того, что это произойдет? Технически, выше нуля, но достаточно близко к нему: существует 2*128 или 340 ундециллионов (10^36) возможных значений uuid4. Достаточно ли это низкие шансы чтобы спать крепко — решать вам.
Одно из главных применений uuid — это Django, имеющий поле UUIDField, которая часто используется как главный ключ в основной реляционной базе данных модуля.
Почему бы просто не использовать SystemRandom по умолчанию?
В дополнению к модулям конфиденциальности, упомянутым в данной статье (таким, как secrets), модуль Python под названием random имеет неприметный класс под названием SystemRandom, который использует os.urandom(). (SystemRandom, в свою очередь, также используется модулем secrets. Все это часть веб, которая возвращается обратно к urandom().)
На этом моменте, вы можете спросить себя, почему просто не использовать эту версию по умолчанию? Почему бы не “всегда быть в безопасности”, вместо того, чтобы пользоваться детерминистическими функциями, которые не являются до конца криптографически безопасными?
Я уже упоминал одну причину: иногда вам нужно, чтобы данные были детерминистическими и воспроизводимыми для других для возможности взаимодействия.
Вторая причина — это то, что CSPRNG (как минимум в Python) ведут себя критично медленнее, чем PRNG. Давайте проверим это со скриптом timed.py, который сравнивает версии randint() у PRNG и CSPRNG, используя timeit.repeat():
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import random import timeit # Наш random “по-умолчанию” на самом деле является экземпляром `random.Random()`. # CSPRNG использует `SystemRandom()` и `os.urandom()` в свою очередь _sysrand = random.SystemRandom() def prng() -> None: random.randint(0, 95) def csprng() -> None: _sysrand.randint(0, 95) setup = 'import random; from __main__ import prng, csprng' if __name__ == '__main__': print('Best of 3 trials with 1,000,000 loops per trial:') for f in ('prng()', 'csprng()'): best = min(timeit.repeat(f, setup=setup)) print('\t{:8s} {:0.2f} seconds total time.'.format(f, best)) |
Теперь выполним это из оболочки:
|
1 2 3 4 |
$ python3 ./timed.py Best of 3 trials with 1,000,000 loops per trial: prng() 1.07 seconds total time. csprng() 6.20 seconds total time. |
Разница во времени в пять раз — определенно сильный аргумент, вкупе с криптографической безопасностью, кода мы выбираем между этими двумя.
Коэффициенты и окончания: Хеширование
Одна концепция, на которую мы не обращали столько внимания в этой статье — это хеширование, которое выполняется при помощи модуля Python под названием hashlib.
Хеш предназначен для одностороннего сопоставления от входного значения до строки с фиксированным размером, которое фактически невозможно для реверсивной инженерии. Таким образом, в то время как результат хеш-функции может выглядеть как случайные данные, это на самом деле не соответствует определению.
Подведем итоги
Мы рассмотрели много нового в данном руководстве. Здесь было приведено детальное сравнение доступных опций для проведения инженерной рандомизации в Python:
| Пакет/Модуль | Описание | Криптографическая безопасность |
| random | Быстрые и простые случайные данные с использованием | Нет |
| numpy.random | Как и random, но для массивов (в т.ч. и для многомерных) | Нет |
| os | Содержит urandom() | Да |
| secrets | Создан модуль для генерации безопасных случайных чисел, байтов и строк | Да |
| uuid | Дом для большого количества функций для создания 128-битных идентификаторов | Да, uuid4() |
Можете оставить совершенно случайные комментарии внизу. Спасибо за ознакомление с материалом!

Являюсь администратором нескольких порталов по обучению языков программирования Python, Golang и Kotlin. В составе небольшой команды единомышленников, мы занимаемся популяризацией языков программирования на русскоязычную аудиторию. Большая часть статей была адаптирована нами на русский язык и распространяется бесплатно.
E-mail: vasile.buldumac@ati.utm.md
Образование
Universitatea Tehnică a Moldovei (utm.md)
- 2014 — 2018 Технический Университет Молдовы, ИТ-Инженер. Тема дипломной работы «Автоматизация покупки и продажи криптовалюты используя технический анализ»
- 2018 — 2020 Технический Университет Молдовы, Магистр, Магистерская диссертация «Идентификация человека в киберпространстве по фотографии лица»
